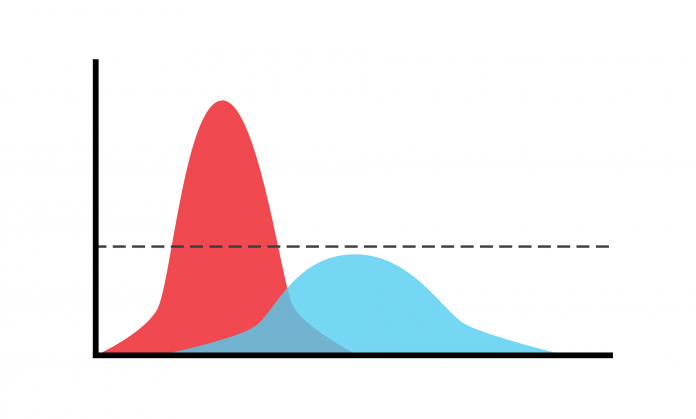
Rarely has a parameter in a model attracted so much attention as the number R – the reproduction rate of covid-19 infection. R is the number of people each infected person infects. If 100 people have the virus, and R is 1.1, then they will pass the infection on to 110 people, who will, in turn, pass it on to 121 people, and so on. The number of the infected soon becomes unmanageably large, and the only respite comes from the hope that people can only be infected once, and so ‘herd immunity’ develops before the whole population falls victim.

Conversely, if R is 0.9, then the initial one hundred infect another ninety, who in turn infect another 81, and the spread quickly disappears. Only 1000 people will ever experience the disease. Thus the critical issue is – is R greater or less than one?
If only it were so easy! The problem is that R is not the same for every individual or every group. Some people spread the disease more than others, perhaps because of their physiology, perhaps because of their lifestyle. There is some suggestion that there may be ‘super spreaders’ – the story of ‘Typhoid Mary’ who infected people far and wide while never suffering herself, is part of medical folklore. And R will be higher for patients and medical staff in hospitals, or cruise line passengers, than for singles in lockdown communicating only through Zoom and Skype.
This dispersion poses two problems for the modeller. Imagine the population consists of two groups, one of which has an R above one and the other has an R below one. The average of groups is not the average for the whole population of which the groups are part. This is sometimes called Simpson’s paradox, but I prefer to return to the old joke about the Scotsman who emigrated to England and thereby raised the average intelligence in both countries.
If the infection is brought under partial control, it is likely that a higher proportion of the infected population will be in the high R group than in the low R group. And if that is so, the average R figure may rise rather than fall. In giving evidence to the Commons Science select committee, Professor Edmunds of the London School of Hygiene and Tropical medicine appeared to be suggesting that this might indeed be what is happening.
The second problem arises from the exponential nature of the spread of disease. Albert Einstein did not in fact say that compound interest is the most powerful force in the universe, but it would not have been a foolish remark. Suppose you invest half your savings in stock one, which grows at 10% per year, and half in stock two, which declines at 10% per year. The average of the two returns is zero – the same as you will earn in the bank today – but in twenty years you will have multiplied your money ninefold. Considerably better than the bank and a reminder that in investment diversity beats certainty.
Unfortunately compounding works against you in epidemiology and disease will spread widely if one group has an R of 1.2 and another an R of 0.6 even though the average is 0.9. The outcome is not quite as extreme as in investment because herd immunity kicks in when so many of the high R group have had the illness that there are few left to be infected. Actually that happens in investment too – no company can grow at 10% per year forever. Life is, of course, more complex still because population groups interact – even under lockdown. Care workers have their own homes to go to; infected people in the community may need to go to hospital.
The lesson is not that models are useless, but that you cannot derive policies – health policies, economic policies, investment allocations, or business strategies – from them. The value of models in these areas is as a means of organising thought, not of making predictions. And quantitative models are only as good as the information that is fed into them. The greatest scandal of this epidemic is the delay in undertaking widespread testing. Even though the random testing now being undertaken sounds wasteful it would have yielded invaluable data if it had commenced much earlier. The cost of obtaining good economic and epidemiological information is trivial relative to the costs of bad policy made in its absence.